Question

Calculate the potential energy at point a

What is the kinetic energy at point B

what is the total mechanical energy of this system

calculate potential energy at point C

what is the kinetic energy at point c

Answer 1

Provided there is no friction, the total energy of the system will remain constant, it will just change between kinetic and potential as the height and speed change. To get the total energy I will assume the box starts at the top of the hill at rest (I don't see the whole problem so I don't really know if this is true)
At the top then, the total system energy is potential only


`E_(total)=E_(potential)=mgh=124kg * 9.8 (m)/(s^2) * 40m =48608J`

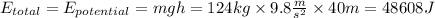
Because point B is at the bottom of the hill, the potential energy is zero, meaning it is all kinetic energy ( in other words, it's moving as fast as it possibly can now) So the kinetic energy is 48608J.

At C the potential energy is


`E_(potential)=mgh=124kg * 9.8 (m)/(s^2) * 25m =30380J`

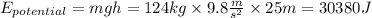
Meaning the rest of the initial energy is the kinetic energy

KE = 48608J - 30380J = 18228J