Question

What is the solution for the two algebraic equations below

3x-2y=25
5y=2x-24
B)-2,7
C)17,2
D)1,-11
A)7,-2
sorry its not in order please help :)

Answer 1

Greetings!

Find the Solution/Point of Intersection:

`\left \{ {{3x-2y=25} \atop {5y=2x-24}} \right.`

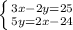Rearrange the System:

`\left \{ {{3x-2y=25} \atop {-2x+5y=-24}} \right.`

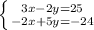Multiply the First Equation by 2 and the Second Equation by 3:

`\left \{ {{2(3x-2y)=2(25)} \atop {3(-2x+5y)=3(-24)}} \right.`


`\left \{ {{6x-4y=50} \atop {-6x+15y=-72}} \right.`

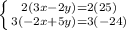
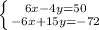Eliminate the x variable:

`+ \frac{\left \{ {{6x-4y=50} \atop {-6x+15y=-72}} \right. }{0x+11y=-22}`


`11y=-22`

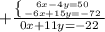
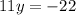Divide both sides by 11:

`(11y)/(11)= (-22)/(11)`


`y=-2`

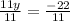
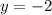Input this value into the First Equation:

`3x-2y=25`


`3x-2(-2)=25`

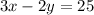
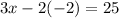Simplify:

`3x+4=25`


`3x=21`

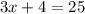
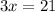Divide both sides by 3:

`(3x)/(3) = (21)/(3)`


`x=7`

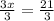
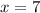The Solution/Point of Intersection is:

`\boxed{(7,-2)}`

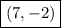
I hope this helped!
-Benjamin