Question

What is the equation of a line with a slope of ​3​ and a point 

(3, 1)
on the line?
Express the equation in the form of
y=mx+b
where m is the slope and b is the y-intercept.

Answer 1

We are already given the slope (3) so we can set that for m.

y = 3x + b

Now all we need is the y-intercept. Using the slope and the ordered pair (3,1), we can calculate at what number the line will cross directly on the y-axis. For the line to cross directly on top of the y axis, the x-value must be 0. When the x equals 0, whatever the y equals is our y-intercept.

Currently the x value is 3. We need to find a way to turn the 0. Use the slope formula (
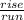
`(rise)/(run)` = 3;
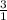
`(3)/(1)` Note: that x equals
`(x)/(1)` ) and reverse it to
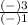
`((-)3)/((-)1)`. Note that the rise deals with the y-value whilst the run deals with the x-value. If it's positive that means +. If it's negative that means -. We turned the slope negative so we could do inverse operations. This let's us find out what the y-value would equal if x was 0.

(3,1) -> (3 - 1, 1 - 3) -> (2, -2) -> (2 - 1, -2 - 3) -> (1,-5) -> (1 - 1, -5 - 3) -> (0,-8).

When x was 0, y was -8. Therefore the y-intercept is -8.

Equation: y = 3x - 8.

View the attachment to see it graphed.

Answer 2

The equation of a line can be written as:

`y - yo = m(x - xo)`
Where (xo, yo)=(3, 1)

`y - 1 = 3(x - 3)`

`y = 3x - 9 + 1`
The equation of the line is:

`y = 3x - 8`