Question

If you transform y = 2x 2 into y = 10x 2, which option below describes the effect of this transformation on the graph of the quadratic function along the y-axis?

Answer 1

The given transformation stretches the graph by a factor of 5.

Explanation:

We have been given that the graph of
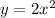`y=2x^2` is transformed into
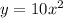`y=10x^2`. We are asked to find the effect of this transformation on the graph of the quadratic function along the y-axis.

Let us recall transformation rules for scaling:

`g(x)\rightarrow ag(x)`

When
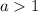`a>1`, the transformation stretches the graph along the y-axis by a factor of a.

When
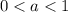`0<a<1`, the transformation compresses the graph along the y-axis by a factor of a.

`g(x)\rightarrow g(ax)`

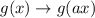
When
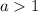`a>1`, the function compressed along the x-axis by a factor of a.

When
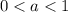`0<a<1`, the function stretched along the x-axis by a factor of a.

Upon looking at our given transformation, we can see that the function is stretched along the y-axis by a factor of 5 as 10 is 5 times 2.

Therefore, our given function is stretched along the y-axis by a factor of 5.

Answer 2

the complete question in the attached figure

y1=2x²

y2=10x²----------------- > y2=5*y1

using a graphic tool-------------------- > see the attached figure

the answer is the option A). The transformation stretches the graph by a factor of 5