Question

The given line segment has a midpoint at (3,1)

What is the equation, in slope-intercept form, of the perpendicular bisector of the given line segment

Answer 1

A

Explanation:

Edge 2020

Answer 2

`y=(1)/(3)x`

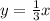
Explanation:

We have been given an image of a line segment and we are asked to find the equation of perpendicular bisector of our given line segment in slope-intercept form.

Since we know that the slope of perpendicular line to a given line is negative reciprocal of the slope of the given line.

Let us find the slope of our given line using slope formula.

`\text{Slope}=(y_2-y_1)/(x_2-x_1)`, where,

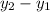`y_2-y_1` = Difference between two y-coordinates,

`x_2-x_1` = Difference between two x-coordinates of same y-coordinates.

Upon substituting the coordinates of points (2,4) and (4,-2) in slope formula we will get,

`\text{Slope}=(-2-4)/(4-2)`

`\text{Slope}=(-6)/(2)`

`\text{Slope}=-3`

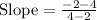
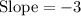
Now we will find negative reciprocal of
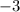`-3` to get the slope of perpendicular line.

`\text{Negative reciprocal of }-3=-(-(1)/(3))=(1)/(3)`

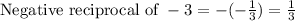
Since point (3,1) lies on the perpendicular line, so we will substitute coordinates of point (3,1) in slope-intercept form of equation
`(y=mx+b)`.

`1=(1)/(3)* 3+b`

`1=1+b`

`1-1=1-1+b`

`b=0`

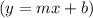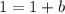
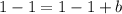
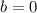
Therefore, the equation of perpendicular line will be
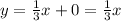`y=(1)/(3)x+0=(1)/(3)x` and option A is the correct choice.