Question

How many half-lives will it take for the concentration of the n2o to reach 30 % of its original concentration?

Answer 1

We have that after 1 half-life, the reactant reaches half its concentration
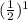
`((1)/(2))^1`. After 2 half-lives it reaches
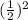
`((1)/(2))^2` of its concentration, namely one-fourth. After n half lives we have that it reaches
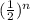
`((1)/(2))^n` of its initial concentration. Thus, we have to solve the equation
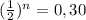
`((1)/(2))^n=0,30`. Taking the log base 2 of each part of the equation we get from logarithm properties:
`log_(2)[(1/2)^n]=log_(2)(2^(-n))=-n`. The other hand yields:
`-n=log_(2)(0,3)`. Solving for n we get that n=1.74. Thus, after around 1.74 half lives the concentration becomes 30% of the initial one. Note how this is consistent with our previous analysis; if we let it a little bit more, 2 half-lives, the concentration will become 25% of the initial.

Answer 2

Number of lives required to reach 30% of the its original concentration is 2.

Step-by-step explanation:

Number of half lives are calculated by using formula :

`a=(a_o)/(2^n)` ............(1)

where,

a = amount of reactant left after n-half lives

`a_o` = Initial amount of the reactant

n = number of half lives

Here we have:

Initial concentration of nitrogen dioxide =
`a_o=x`

Concentration of nitrogen dioxide after n number of half lives = a

a = 30% of x :

`(30)/(100)* x= 0.3x`

`a=(a_o)/(2^n)`

`0.3x=(x)/(2^n)`

`2^n=(1)/(0.3)`

n = 1.736 ≈ 2

Number of lives required to reach 30% of the its original concentration is 2.