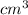Answer:
i. Curved surface area = 2310
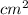
ii. Total surface area = 3696
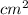
iii. volume = 12936
Explanation:
Perimeter of the circular base = circumference of the circle = 132 cm
circumference of a circle = 2
 r
r
132 = 2
 r
r
r =

=
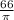
r = 66 x
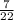
= 3 x 7
= 21
radius = 21 cm
vertical height, h = 28 cm
Thus applying the Pythagoras theorem,
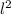 =
=
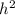 +
+
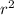
=
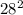 +
+
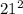
= 784 + 441
= 1225
l =
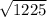
l = 35 cm
The slant height is 35 cm.
i. Curved surface area =
 rl
rl
=
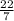 x 21 x 35
x 21 x 35
= 22 x 3 x 35
= 2310
curved surface area of the cone is 2310
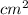 .
.
ii. Total surface area =
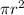 +
+
 rl
rl
=
 r(r + l)
r(r + l)
=
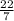 x 21 (21 + 35)
x 21 (21 + 35)
= 22 x 3 x 56
= 3696
The total surface area of the cone is 3696
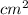 .
.
iii. volume of a cone =

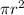 h
h
=
 x
x
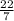 x
x
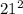 x 28
x 28
= 12936
The volume of the cone is 12936