Question

Two fishing boats depart a harbor at the same time, one traveling east, the other south. the eastbound boat travels at a speed 3 mi/h faster than the southbound boat. after 3 h the boats are 45 mi apart. find the speed of the southbound boat.

Answer 1

1) Let's call
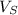
`V_S` the speed of the southbound boat, and
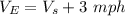
`V_E=V_s+3~mph` the speed of the eastbound boat, which is 3 mph faster than the southbound boat. We can write the law of motion for the two boats:

`S_E(t)=V_E t=(V_S+3)t`

`S_S(t)=V_S t`


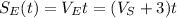
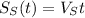
2) After a time
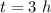
`t=3~h`, the two boats are
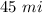
`45~mi` apart. Using the laws of motion written at step 1, we can write the distance the two boats covered:

`S_E(3~h)=3(V_S+3)=3V_S+9`

`S_S(3~h)=3V_S`
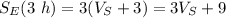
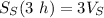
The two boats travelled in perpendicular directions. Therefore, we can imagine the distance between them (45 mi) being the hypotenuse of a triangle, of which
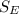
`S_E` and
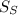
`S_S` are the two sides. Therefore, we can use Pythagorean theorem and write:

`45= √((3V_S)^2+(3V_S+9)^2)`
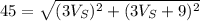
Solving this, we find two solutions. Discarding the negative solution, we have
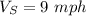
`V_S=9~mph`, which is the speed of the southbound boat.