Question

Frank purchased his house 16 years ago by taking out a 25-year mortgage for $150,000. the mortgage has a fixed interest rate of 5 percent compounded monthly. if he wants to pay off his mortgage today, how much money does he need? he made his most recent mortgage payment earlier today.​

Answer 1

Answer: Since Frank made his most recent EMI payment today, Frank needs 76,136.52 in order to pay off his mortgage today.

We follow these steps to arrive at the answer:

We first calculate the EMI on loan taken out:

The EMI is nothing but P (constant amount paid or received periodically) in the Present Value of an Annuity formula. The formula is

`\mathbf{PV_(Annuity) = EMI* \left[ (1 - (1+r)^(-n))/(r) \right]}`

Substituting the values from the question we get,

150000 = EMI* \left[ \frac{1 - (1+\frac{0.05}{12})^{-(25*12)}}{\frac{0.05}{12}} \right]

Solving we get,

`150000 = EMI* \left[\171.06\right]`

`(150000)/(171.060047) = EMI`

`\mathbf{EMI = 876.8850623}`

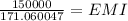
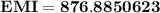
We then construct the Amortization table attached below. At the end of 16 years or 192 periods (
`16*12`), we can see that the principal outstanding is $76,136.52.

Answer 2

The current value of the mortgage will be given by:
A=P(1+r/100)^n
where:
P=$150,000
r=5%
n=16 years
therefore:
A=150000(1+5/100)^16
A=150000(1.05)^16
A=$201,014.35
If He wants to pay off his mortgage now, he needs $201,014.35