Question

Three galaxies are aligned along an axis in order a, b,

c. an observer in galaxy b is in the middle and observes that galaxies a and c are moving in opposite directions away from him, both with speeds 0.63c. what are the speeds of galaxies b and c as observed by someone in galaxy a?

Answer 1

This is a somewhat tricky question. Our universe is constantly expanding. Ignoring small gravitational effects, if we are centered at a galaxy and look around us, every other galaxy should be moving away from us. Nevertheless, there is no central point in our expansion. Imagine dots on a balloon; as we blow the balloon, all points distance themselves from the others, with no point being central. The speed of this "expansion" is given by Hubble's law: u=H*d where u is the speed with which a galaxy is moving away from us, d is our distance to that galaxy and H a univeral constant, Hubble's constant. This helps us with the first question; A will see B recede with an equal speed from it, 0,63c. We have from the geometry of the situation that
`d_(AB) + d_(BC) =d_(AC)`.
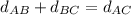
`u_(AC) =H* d_(AC)` also holds. Now, substituting in our distance equation and using Hubble's law, we get that
`u_(AC)=u_(AB)+u_(BC)=1.26c`. Thus, A will see galaxy C receding at a speed of 1.26c. This is not against the theory of relativity, but it is a very mathematical point; do not worry about your speed being higher than the speed of light!