Answer:
The solutions to
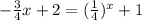 are (0,2) and (1,1.25).
are (0,2) and (1,1.25).
Explanation:
Given : The functions
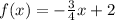 and
and
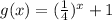 are shown in the graphs.
are shown in the graphs.
To find : What are the solutions to
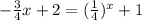 ?
?
Solution :
Expression
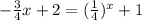 means f(x)=g(x)
means f(x)=g(x)
We know that, If two functions are equal then there solution is the intersection point of the curves.
When we determine the graph the intersection points are (0,2) and (1,1.25).
Refer the attached figure for clearance.
Therefore, The solutions to
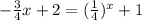 are (0,2) and (1,1.25).
are (0,2) and (1,1.25).