Question

Calculate the standard electrode potential difference (e°) of the daniell cell (at 1 bar) if temperature is 473.15 k.

Answer 1

Missing data in the text of the exercise: The molar concentration of Zinc is 10 times the molar concentration of copper.

Solution:

1) First of all, let's calculate the standard electrode potential difference at standard temperature. This is given by:

`E^0=E_(cat)^0-E_(an)^0`
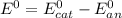
where
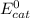
`E_(cat)^0` is the standard potential at the cathode, while
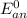
`E_(an)^0` is the standard potential at the anode. For a Daniel Cell, at the cathode we have copper:
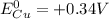
`E_(Cu)^0=+0.34 V`, while at the anode we have zinc:
`E_(Zn)^0=-0.76 V`. Therefore, at standard temperature the electrode potential difference of the Daniel Cell is

`E^0=+0.34 V-(-0.76 V)=+1.1 V`

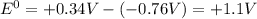
2) To calculate
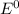
`E^0` at any temperature T, we should use Nerst equation:

`E^0(T)=E^0- (R T)/(z F) \ln ([Zn])/([Cu])`
where

`R=8.31 J/(K mol)`

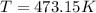
`T=473.15 K` is the temperature in our problem

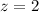
`z=2` is the number of electrons transferred in the cell's reaction

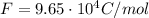
`F=9.65\cdot 10^4 C/mol` is the Faraday's constant

`[Zn]` and
`[Cu]` are the molar concentrations of zinc and in copper, and in our problem we have
`[Zn]=10[Cu]`.
Using all these data inside the equation, and using
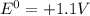
`E^0=+1.1 V`, in the end we find:

`E^0(T)=E^0- (R T)/(z F) \ln ([Zn])/([Cu])=+1.053 V`