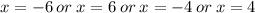ANSWER
The solutions are,
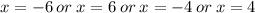
Step-by-step explanation
The given polynomial equation is,
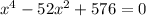
We can rewrite the equation to obtain,
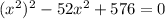
If we let
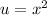
Then our equation becomes,
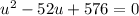
This is a quadratic equation that can be solved by factoring.
We split the middle term to obtain,
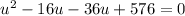
This factors to give us,
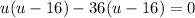
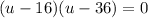
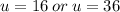
This implies that,
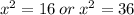

There real solutions are,