First, we claim that
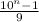
is the
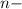
digit number with all digits equal to one.
Note that

is a one followed by

zeroes, so subtracting one gives

nines. Divide that number by nine and you get

ones, completing the proof.
Therefore, we have that
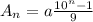
,
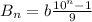
, and
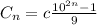
.
Let
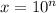
. Then, we have:
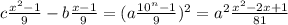
.
Multiplying by
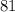
gives:
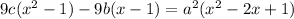
Now, note that
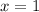
is not a valid input, since
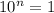
requires
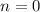
, so we safely divide by
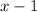
to get:
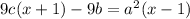
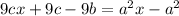
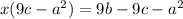
Because this is now a linear equation in

, it has either zero, one, or infinitely many solutions. Obviously, we need the latter to occur, which happens when

and
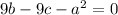
, since the coefficient of

must cancel to zero and thus the RHS must equal zero as well.
Since
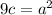
, we must have
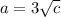
. Since

must be a multiple of three, we plug in values. If

, we get
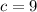
and thus
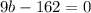
, which is impossible. So

doesn't work.
With
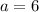
,
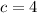
, and thus
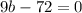
, so
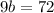
, so
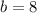
. This gives
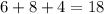
as one possibility.
With
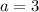
,
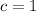
, and thus
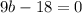
, so
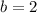
. This obviously is worse.
We've gone through all the cases and the two possibilities are
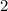
and
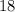
, so our answer is
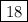
.