Question

Let a and b be real numbers where a b 0. Which of the following functions could represent the graph below?

#y
○_f(x) = x(x − a)²(x −b)4
f(x) = x(x − a)³(x − b)²
f(x) = x²(x-a)(x - b)²
O f(x) = x²(x-a)5(x - b)
X

Answer: C
f(x)= x^4(x-a)(x-b)^2

Answer 1

`f(x)=x^4(x-a)(x-b)^2`

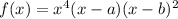
Explanation:

The graph of a polynomial function will:

• touch the x-axis at zeros with even multiplicities.
• cross the x-axis at zeros with odd multiplicities.

The zero at the origin (0, 0) touches the x-axis and so it has an even multiplicity (exponent). Therefore, we can immediately discount the first two answer options as both have x as a zero (x = x¹ so its exponent is odd).

The end behavior of the graphed function means the leading coefficient is positive and the degree of the polynomial is odd.

The sum of the multiplicities is the degree of the polynomial function.

`f(x)=x^4(x-a)(x-b)^2 \implies \textsf{Sum of multiplicities}: 4+1+2=7`

`f(x)=x^2(x-a)^5(x-b) \implies \textsf{Sum of multiplicities}: 2+5+1=8`

Therefore, the only function that could represent the given graph is

`\boxed{f(x)=x^4(x-a)(x-b)^2}`

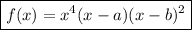
as its degree is odd and it has a zero at the origin with even multiplicity.