Question

Which is one of the transformations applied to the graph of f(x)=x^to change it into the graph of g(x)=4x^+24x+30

Answer 1

Problem:
Find one of the transformations applied to the parent function f(x)=x^2 to change it into the graph g(x)=4x^2+24x+30.

Steps
1. Use completing square to transform g(x) into vertex form:

`g(x)=4x^2+24x+30`

`=4(x^2+6x+7.5)`

`=4((x+3)^2-9+7.5)`

`= 4((x+3)^2 - 1.5)`

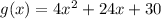
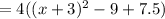
2. Match above function g(x) with a transformed function of f(x), with vertical stretch factor a, horizontal translation h, and vertical translation k:

`g(x)=a f(x-h) + k`

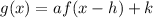
3. By comparison, we see that
a=4,
h=-3
k=4(-1.5)=-6

So the three steps (any one of which should do for the answer) are:
translate left 3 units
vertical stretch 4 units
vertical translation -6 units.

Answer 2

The graph of f(x) = x^2 is shifted left 3 units.

Explanation: