Question

The dilation rule DF,3(x, y) is applied to △ABC, where the center of dilation is at F(1, 1). The distance in the x-coordinates from A(–2, 2) to the center of dilation F(1, 1) is unit(s). The distance in the y-coordinates from A(–2, 2) to the center of dilation F(1, 1) is unit(s). The vertex A' of the image is .

Answer 1

3

1

(-8,4)

Explanation:

Answer 2

The distance between x-coordinates of A and F is 3 units.The distance between y-coordinates of A and F is 1 unit. The coordinates of A' are (-8,4).

Explanation:

The dilation rule is
`D_(F,3)(x,y)`.

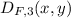It means the center of dilation is F and scale factor is 3.

The coordinates of A are (-2,2) and the coordinates of F are (1,1).

The distance in the x-coordinates from A(–2, 2) to the center of dilation F(1, 1) is

`-2-1=-3`

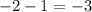
The distance can not be negative. So, the distance between x-coordinates of A and F is 3 units.

The distance in the y-coordinates from A(–2, 2) to the center of dilation F(1, 1) is

`2-1=1`

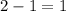
The distance between y-coordinates of A and F is 1 unit.

According to given dilation rule,

`(x,y)\rightarrow (3(x-1)+1,3(y-1)+1)`

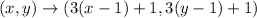
The coordinates of A' are

`A(-2,2)\rightarrow A'(3(-2-1)+1,3(2-1)+1)`

`A(-2,2)\rightarrow A'(3(-3)+1,3(1)+1)`

`A(-2,2)\rightarrow A'(-8,4)`

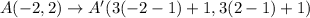
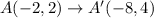
Therefore the distance between x-coordinates of A and F is 3 units.The distance between y-coordinates of A and F is 1 unit. The coordinates of A' are (-8,4).