Given:
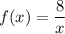
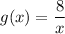
To find:
Whether f(x) and g(x) are inverse of each other by using that f(g(x)) = x and g(f(x)) = x.
Solution:
We know that, two function are inverse of each other if:
 and
and
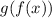
We have,
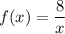
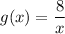
Now,
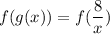
![[\because g(x)=(8)/(x)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/g9bs4auh9hzlgff480kbig3uzhnvh8nup1.png)
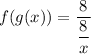
![[\because f(x)=(8)/(x)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/81vhro5wirfko5hnk0nag5gd6mwwqa331x.png)
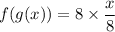

Similarly,
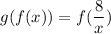
![[\because f(x)=(8)/(x)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/81vhro5wirfko5hnk0nag5gd6mwwqa331x.png)
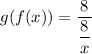
![[\because g(x)=(8)/(x)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/g9bs4auh9hzlgff480kbig3uzhnvh8nup1.png)
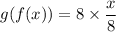

Since,
 and
and
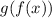 , therefore, f(x) and g(x) are inverse of each other.
, therefore, f(x) and g(x) are inverse of each other.