Question

Giovanni has a dog enclosure that is 6 feet by 10 feet in his backyard. He wants to double the area of the enclosure by increasing the length and the width by the same amount. By how many feet will the length and the width be increased? Round to the nearest hundredth if necessary.

Answer 1

12 feet by 20 feet...

Answer 2

The number of feet by which the length and width is increased is:

3.14 feet

Explanation:

Giovanni has a dog enclosure that is 6 feet by 10 feet in his backyard.

The area of the enclosure is: 6×10=60 square feet

Now let x be the amount by which the length and width of the enclosure is increased.

i.e. the length is: 6+x

and width is: 10+x

Also, the new area of the enclosure is:

`(6+x)\cdot (10+x)=2* 60\\\\\\i.e.\\\\\\x^2+16x+60=120\\\\\\i.e.\\\\\\x^2+16x+60-120=0\\\\\\i.e.\\\\\\x^2+16x-60=0`

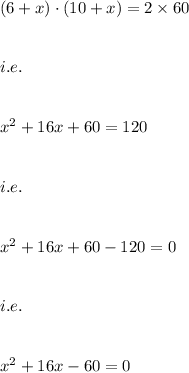
On solving using the quadratic formula

( i.e. any quadratic equation of the type:

`ax^2+bx+c=0`

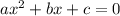
the solution is given by:

`x=(-b\pm √(b^2-4ac))/(2a)` )

Here we have: a=1 and b=16 and c= -60

We get the solution as:

`x=(-16\pm √((16)^2-4* (-60)* 1))/(2)\\\\\\x=(-16\pm √(256+240))/(2)\\\\\\x=(-16\pm √(496))/(2)\\\\\\x=(-16\pm 22.2710)/(2)`

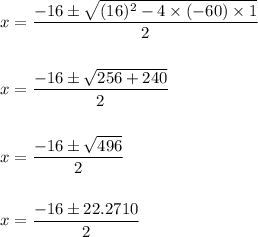
i.e.
`x=-19.136\ and\ x=3.136`

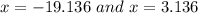
x can't be negative as it is the amount of distance.

Hence, to the nearest hundredth we have:

x=3.14

Hence, the answer is:

3.14 feet