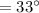Question

What is the measure of AC ?

Enter your answer in the box.


°

Answer 1

Answer:
`33^(\circ)`

Explanation:

We know that, the inscribed angle theorem says that the measure of an inscribed angle is exactly half the measure of its intercepted arc.

In the given picture , the inscribed angle = (2.5x+4)°

The intercepted arc = (7x-2)°

Then by inscribed angle theorem , we have

`(2.5x+4)=(1)/(2)*  (7x-2)\\\\\Rightarrow\ 2(2.5x+4)=7x-2\\\\\Rightarrow\ 5x+8=7x-2\\\\\Rightarrow\ 7x-5x=8+2\\\\\Rightarrow\ 2x=10\\\\\Rightarrow\ x=(10)/(2)=5`

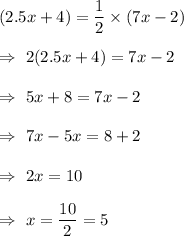
Now, the measure of
`\overarc{AC}=(7x-2)^(\circ)=(7(5)-2)^(\circ)=(35-2)^(\circ)`

`=33^(\circ)`

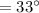
Hence, the measure of arc AC
`=33^(\circ)`

Answer 2

we are given that

Inscribed angle
`=(2.5x+4)`

Intercepted arc
`=(7x-2)`

As we know that the Inscribed angle is Half of the measure of the intercepted arc.

So we can write

`(2.5x+4)=(1)/(2)(7x-2) \\\\7x-2=2(2.5x+4)\\\\7x-2=5x+8\\\\7x-5x=8+2\\\\2x=10\\\\x=5\\\\\text{So Measure of arc AC}=(7x-2)=7*5-2=35-2=33`