Question

A solid right pyramid has a regular hexagonal base with an area of 7.4 units2. The pyramid has a height of 6 units. What is the volume of the pyramid

Answer 1

`14.8\text{ Units}^3`

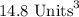
Explanation:

We have been given that the base area of a right pyramid with hexagonal base is 7.4 square units. The pyramid has a height of 6 units.

To find the volume of the given pyramid we will use formula:

`\text{Volume of hexagonal pyramid}=\text{ Base area}* \frac{\text{Height}}{3}`

`\text{Volume of hexagonal pyramid}=7.4\text{ Units}^2* \frac{\text{6 units}}{3}`

`\text{Volume of hexagonal pyramid}=7.4\text{ Units}^2* \text{2 units}`

`\text{Volume of hexagonal pyramid}=14.8\text{ Units}^3`

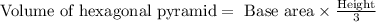
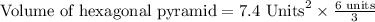
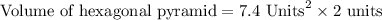
Therefore, the volume of given hexagonal pyramid is 14.8 cubic units.

Answer 2

14.8 cubic units

Explanation:

The volume of the right pyramid can be calculated using formula

`V_(pyramid)=(1)/(3)\cdot A_(base)\cdot height.`

You are given

`A_(base)=7.4\ un^2.\\ \\height=6\ un.`

Then

`V_(pyramid)=(1)/(3)\cdot 7.4\cdot 6=2\cdot 7.4=14.8\ un^3.`