Question

write the equation of the line that passes through the point (6,2) and is perpendicular to a line that passes through the points (-5,3) and (-1,-9

Answer 1

y - 2 = ¹/₃(x - 6) ← the point-slope form of the equation

y = ¹/₃x ← the slope-intercept form of the equation

x - 3y = 0 ← standard form of the equation

Explanation:

The slope of line that passes through (-5, 3) and (-1, -9):

`m_0=(3-(-9))/(-5-(-1))=(3+9)/(-5+1)=(12)/(-4)=-3`

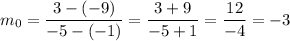
The slope of a line perpendicular to the line with the slope m₀:

`m=-\frac1{m_0}=-\frac1{-3}=\frac13`

The point-slope form of the equation of a line: y - y₁ = m(x - x₁), where m is the slope and (x₁, y₁) is the point the line passing through.

(6, 2) ⇒ x₁ = 6, y₁ = 2

So:

y - 2 = ¹/₃(x - 6) ← the point-slope form of the equation

y - 2 = ¹/₃x - 2 {add 2 to both sides}

y = ¹/₃x ← the slope-intercept form of the equation

y - ¹/₃x = 0 {multiply both sides by (-3)}

x - 3y = 0 ← standard form of the equation