Question

Mensa is a society for "geniuses." one way to qualify for membership is having an iq at least 2.5 standard deviations above average. iqs are approximately normally distributed, according to the wais scale. what percent of people should qualify?

Answer 1

For 2.5 standard deviations above the average, only 0.621% should qualify for membership at Mensa.

Step-by-step explanation:

To answer this question, we need to make use of some concepts:

1. The meaning of the standard normal distribution.
2. The purpose of the cumulative standard normal distribution.
3. The z-scores.

Standard normal distribution

We can obtain the probabilities for any normal distribution using the values of the standard normal distribution, which are given by the cumulative distribution function, and we can also consult all these values, by general, from the cumulative standard normal table using z-scores.

Z-scores

A z-score is a "transformation" of a "raw" value using the next formula:

`\\ z = (x - \mu)/(\sigma)` (1)

Where

x is a normally distributed value to be transformed in a z-score.

`\\ \mu\;is\;the\;population\;mean`.

`\\ \sigma\;is\;the\;population\;standard\;deviation`.

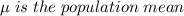Well, a z-score, as we can see from (1) represents how far are the values from the population mean in terms of standard deviations. When a z-score is positive, it means that the value of the raw score is above the mean, whereas a negative value indicates that the raw score is below the mean.

2.5 Standard Deviations and Solution

Therefore, 2.5 standard deviations above the mean is a z-score = 2.5.

Consulting the cumulative standard normal table, a z-score = 2.5 has a cumulative probability P(z<2.5) = 0.99379 (from negative infinity to this value).

Then, to determine the probability for P(z>2.5), that is, the probability for those values greater than 2.5 standard deviations (Mensa membership), we need to subtract from 1 the probability P(z<2.5) (because the sum of all probabilities equals 1, and we are looking for the remaining probability), or mathematically:

`\\ P(z>2.5) = 1 - P(z<2.5) = 1 - 0.99379 = 0.00621`

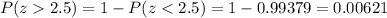
Or P(z>2.5) = 0.621%.

In words, only 0.621% of people have IQs 2.5 standard deviations above the mean and should qualify for membership at Mensa.

Answer 2

According to the scale, an average person would posses the mean of 100 IQ and standard deviation of 15. If to be a member of mensa one should have an iq at least 2.5 standard deviations above average, the minimum iq should be:

2.5 = (x-100)/15

x = 137.5 >>>>> Less than 1% population belong to this IQ group or higher.