Question

What is the maximum distance we can shoot a dart, provided our toy dart gun gives a maximum initial velocity of 5.84 m/s?

Answer 1

1) The maximum distance can be reached when the dart is shot with an angle of
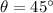
`\theta=45^(\circ)` above the horizontal (see demonstration of this fact at the end).

2) The motion of the dart is an uniform motion on the x-axis (horizontal direction) with constant velocity
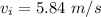
`v_i = 5.84~m/s` and it is an uniformly accelerated motion on the y-axis (vertical direction), with the gravitational acceleration
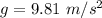
`g=9.81~m/s^2` acting downwards. So we can write the laws of motion on both directions:

`S_x(t) =( v_i cos(\theta)) t`

`S_y(t) = (v_i sin(\theta))t - (1)/(2) gt^2`
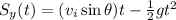
where the negative sign means that g points downwards.

3) First of all we can find the time at which the dart reaches the ground. This can be found by requiring
`S_y(t)=0`:

`(v_i sin(\theta))t - (1)/(2) gt^2=0`
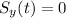
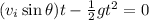
From this we find two solutions:
`t=0~s`, corresponding to the beginning of the motion (so we are not interested in this one), and

`t= (2 v_i sin(\theta))/(g) =0.84~s`

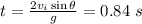
4) Now that we now when the dart reaches the ground, we can use this information to find the distance covered on the x-axis, by using
`t=0.84~s` inside the equation of
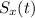
`S_x(t)` written at point 2:

`S_x(0.84~s)= 5.84~m/s \cdot \cos{45^(\circ)} \cdot 0.84~s }=3.47~m`

--------------------------
DEMONSTRATION OF POINT 1:

Calling v the initial velocity of the dart, and using a coordinate system where the x-axis coincides with the horizontal direction and the y-axis with the vertical direction, we can write the law of motion on both directions:

`S_x(t) = v cos{\theta} t`

`S_y(t) = v sin{\theta} t + (1)/(2) g t^2`
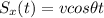
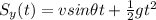
where t is the time,
`\theta` is the initial angle of the dart, and
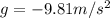
`g= -9.81 m/s^2` is the gravitational acceleration.
The maximum horizontal distance can be found by requiring that
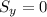
`S_y=0`. This condition occurs twice: when the motion starts (
`t=0`) and when the dart falls to the ground (let’s call
`t_s` the time at which this happens). Therefore we can find
`t_s` by requiring
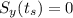
`S_y(t_s)=0`, i.e.:

`v sin{\theta} t_s + (1)/(2) g t_s^2 =0`
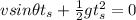
which has two solutions:
`t_s=0` (beginning of the motion) and
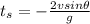
`t_s = - \frac{2 v sin{\theta}}{g}`.So we can find the maximum horizontal distance covered by the dart by substituting this
`t_s` into the law of motion for
`S_x(t)`:

`S_x(t_s) =  v cos\theta t_s = -(2 v^2 cos\theta sin\theta)/(g)`
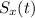
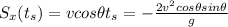
Since

`sin2\theta = 2 cos\theta sin\theta`,
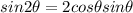
we can write

`S_x(t_s) = - (v^2 sin2\theta)/(g)`
Since g is negative, the maximum of this function occurs for
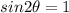
`sin2\theta=1`, and this happens when
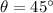
`\theta=45^(\circ)`.