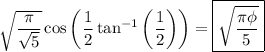A rather lengthy solution using a neat method I just learned relying on complex analysis.
First observe that
![e^(-x^2) \cos(2x^2) = \mathrm{Re}\left[e^(-x^2) e^(i\,2x^2)\right] = \mathrm{Re}\left[e^(a x^2)\right]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/cfkba0fx3zujz894ip6o.png)
where
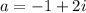 .
.
Normally we would consider the integrand as a function of complex numbers and swapping out
 for
for
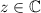 , but since it's entire and has no poles, we cannot use the residue theorem right away. Instead, we introduce a new function
, but since it's entire and has no poles, we cannot use the residue theorem right away. Instead, we introduce a new function
 such that
such that
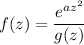
has at least one pole we can work with, along with the property (1) that
 has period
has period
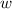 so
so
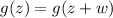 .
.
Now in the complex plane, we integrate
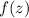 along a rectangular contour
along a rectangular contour
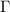 with vertices at
with vertices at
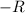 ,
,
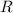 ,
,
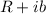 , and
, and
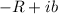 with positive orientation, and where
with positive orientation, and where
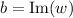 . It's easy to show the integrals along the vertical sides will vanish as
. It's easy to show the integrals along the vertical sides will vanish as
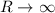 , which leaves us with
, which leaves us with
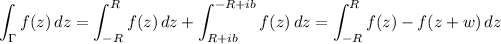
Suppose further that our cooked up function has the property (2) that, in the limit, this integral converges to the one we want to evaluate, so
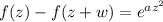
Use (2) to solve for
 .
.
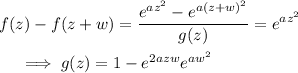
Use (1) to solve for the period
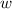 .
.
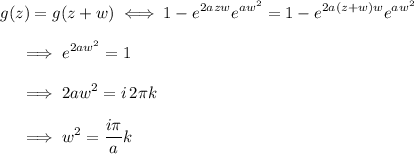
Note that
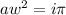 , so in fact
, so in fact
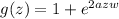
Take the simplest non-zero pole and let
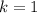 , so
, so
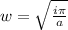 . Of the two possible square roots, let's take the one with the positive imaginary part, which we can write as
. Of the two possible square roots, let's take the one with the positive imaginary part, which we can write as

and note that the rectangle has height
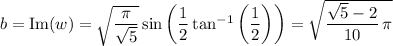
Find the poles of
 that lie inside
that lie inside
 .
.

We only need the pole with
 , since it's the only one with imaginary part between 0 and
, since it's the only one with imaginary part between 0 and
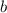 . You'll find the residue here is
. You'll find the residue here is
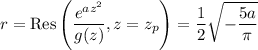
Then by the residue theorem,
![\displaystyle \lim_(R\to\infty) \int_(-R)^R f(z) - f(z+w) \, dz = \int_(-\infty)^\infty e^((-1+2i)z^2) \, dz = 2\pi i r \\\\ ~~~~ \implies \int_(-\infty)^\infty e^(-x^2) \cos(2x^2) \, dx = \mathrm{Re}\left[2\pi i r\right] = \sqrt{\frac\pi{\sqrt5}} \cos\left(\frac12 \tan^(-1)\left(\frac12\right)\right)](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/2agsqbjnl8tyv8ai6r27.png)
We can rewrite
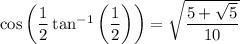
so that the result is equivalent to