Question

Train car A is at rest when it is hit by Train car B. The two cars, which have the same mass, stick together and move off after the collision. How does the final velocity of train cars A and B after the collision compare to the initial velocity of train car B before the collision?

A. The final velocity is double train car B's initial velocity.
B. The final velocity is the same as train car B'd initial velocity.
C. The final velocity is half of train car B's initial velocity.
D. The final velocity is zero, since train car B will stop.

Answer 1

C is right

Just took it

Answer 2

C. The final velocity is half of train car B's initial velocity.

Step-by-step explanation:

Let's solve the problem by using the law of conservation of momentum.

The initial momentum of the system is:

`p_i = m u_B`

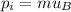
where m is the mass of car B (equal to the mass of car A) and
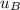`u_B` is the initial velocity of car B. There is no contribution to the momentum from car A, since car A is at rest, so its momentum is zero.

The momentum of the system after the collision is:

`p_f = (m+m)v=2mv`

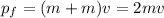
where we wrote (m+m) because now both cars travel together, so their new mass is (m+m), and v is their final velocity.

By using conservation of momentum:

`p_i = p_f`

`m u_B = 2 m v`

`v=(u_B)/(2)`

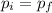
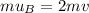
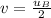
so, the final velocity is half of train car B's initial velocity.