The principal is
P = $24
Calculate the duration.
t = 2014 - 1626 = 388 years
The value after 388 years is
A = $6 x 10⁹
For continuous compounding, the compounding interval is
n = 365
Let r = the rate.
Then use the formula
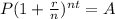
That is,
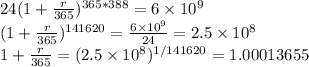
Hence obtain
r/365 = 1.00013655 - 1 = 0.00013655
r = (0.00013655)*(365) = 0.0498 = 4.98%
Answer: 5.0% (to 1 decimal place)