If you're familiar with synthetic division, but not the extended form (which allows you easily compute the quotient/remainder when dividing a polynomial by another polynomial of degree greater than 1), then you can perform two steps of SD.
Instead of dividing by
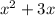
, first divide by

, then by
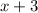
(since

). So we have
0 | 1 4 2 1 4
... | 0 0 0 0
= = = = = = = = = = = =
... | 1 4 2 1 4
which translates to
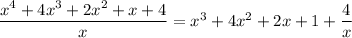
Ignoring the remainder term for now, the next round of SD yields
-3 | 1 4 2 1
... | -3 -3 3
= = = = = = = = = =
... | 1 1 -1 4
which translates to

Now, putting everything together, we have


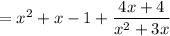
which is to say the remainder upon dividing
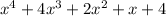
by
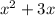
is
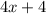
.