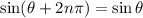Question

Please Helppp Cacl AB Determining Slopes.

Answer 1

The zeros of the function are those values of
`x` that make
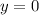
`y=0`. So we solve


`0=(1+50\sin x)/(x^2+3)`

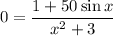
The denominator will always be positive, so we can multiply both sides of the equation by it to get


`0=1+50\sin x\implies \sin x=-\frac1{50}`

`\implies x=\arcsin\left(-\frac1{50}\right)+2n\pi=-\arcsin\frac1{50}+2n\pi`

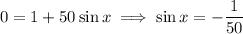
where
`n` is any integer. If we take
`n=\pm1` we should get the two solutions immediately adjacent to the one near
`x=0` that still lie in the interval
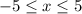
`-5\le x\le5`. So the other two zeros are
`x=-\arcsin\frac1{50}\pm\pi`.

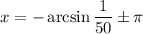
The tangent line to the curve at any
`x` is determined by the value of the derivative of the function at that value of
`x`. So first compute the derivative:




Now just plug in the values of
`x` determined above. It's helpful to note


`\cos\left(\arcsin\frac1{50}\right)=(7√(51))/(50)`

`\cos(\theta+2n\pi)=\cos\theta`

`\sin(\theta+2n\pi)=\sin\theta`