Question

You have a fishing line spool with an end that has an area of 20.0 cm2. how much fishing line do you need to wind around the spool 10 times?

Answer 1

The provided solution calculates the linear length of fishing line that is paid out from a spool as a result of rotational motion, yielding 9.90 meters of line when the spool rotates at 220 radians.

Step-by-step explanation:

The question is asking for the length of fishing line needed to wrap around a spool with a specified surface area. In the reference solution provided, the linear amount of fishing line played out is directly related to a rotational motion described by the radius of the spool (r) and the angular rotation (θ) in radians. Given the value for rotation at 220 radians per second and a spool radius of 0.045 meters, the length of the line unwound is calculated as:

x = rθ = (0.0450 m)(220 rad) = 9.90 m.

This calculation translates a rotational motion into a linear distance, demonstrating the connection between linear and rotational quantities in physics.

Answer 2

Answer: 158.53 cm

Step-by-step explanation:

We know that the ends of a fishing line spool are circular in shape.

Given : The area of an end of fishing line spool =
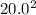`20.0\cm^2` (1)

Area of a circle =
`\pi r^2` (2)

Circumference of a circle =
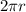`2\pi r` (3)

, where r is radius of the circle.

From (1) and (2), we have

`\pi r^2=20\\\\\Rightarrow\ r^2=(20)/(\pi)\\\\\Rightarrow\ r=\sqrt{(20)/(\pi)}`

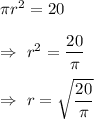
Circumference of fishing spool =
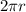`2\pi r` (using (3))

`=2\pi \sqrt{(20)/(\pi)}=2√(20\pi)=2*2√(5\pi)=4√(5\pi)`

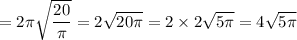
i.e. Fishing spool required to wind around the spool one time
`=4√(5\pi)\ cm`

⇒ Fishing spool required to wind around the spool 10 times
`=10*4√(5\pi)\ cm=40√(5\pi)\\\\=40*√(5)* \pi\\\\=40*2.236*√(3.14159)\\\\=89.44*1.772453\\\\=158.528205473\approx158.53\ cm`

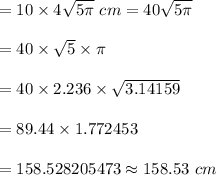
Hence, you need 158.53 cm or about 159 cm of fishing line to wind around the spool 10 times.