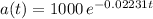Question

A 1000 gallon tank, initially full of water, develops a leak at the bottom. given that 200 gallons of water leak out in the first 10 minutes, find the amount of water, a(t), left in the tank t minutes after the leak develops if the water drains off at a rate proportional to the amount of water present.

Answer 1

Let a = amount of water (gallons) in the tank at time t (minutes).

The drainage rate is proportional to the amount of water left in the tank, therefore

`(da)/(dt) = ka`
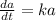
where k is the proportionality constant.
Therefore, obtain

`(da)/(a) =k\, dt`
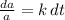
Integrate to obtain
ln(a) = kt + c.
where c = the constant of integration.

When t = 0, a = 1000 gal, therefore
ln(1000) = c
When t = 10 min, then a = 1000 - 200 = 800 gal.
Therefore
ln(800) = 10k + ln(1000)
10k = ln(800) - ln(1000) = -0.2231
k = -0.02231

Therefore
ln(a) = -0.02231t + ln(1000)
ln(a/1000) = -0.02231t

`a(t) = 1000\,e^(-0.02231t)`
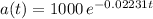
A graph of the solution is shown below.

Answer:
`a(t) = 1000 \, e^(-0.02231t)`

Answer 2

Let the amount of water remaining be a, then: da/dt = -ka, since the rate of loss of water is proportional to the amount remaining in the tank, with k as proportionality constant.
Solving the equation gives: da/a = -kdt
Integrating: ln(a0 / a) = kt
Substituting the given a0 = 1000 gallons and a = 800 gallons (since 200 has leaked out) at the given t = 10 minutes:
ln(1000 / 800) = 10k
k = 0.0223 (rate constant)
Then we substitute back into the equation to get:
ln(1000 / a) = 0.0223t
1000 / a = e^(0.0223t)
a = 1000e^(-0.0223t)