Answer:
Part A) The length of rectangle is

Part B) The perimeter of the square is

Part C)
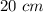
Part D)
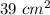
Explanation:
Part A) Find the length of the rectangle
we know that
The perimeter of rectangle is equal to
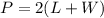
we have
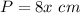
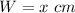
substitute and solve for L
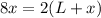
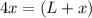
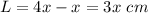
Part B) Find the perimeter of the square
we know that
The perimeter of a square is
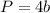
we have that
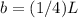
substitute the value of L
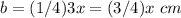
Find the perimeter of the square
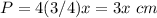
Part C) Find how many cm greater the rectangle's perimeter than the square's perimeter if x=4
Find the value of rectangle's perimeter
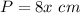 ------>
------>
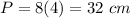
Find the value of square's perimeter
 ------>
------>
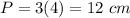
Find the difference
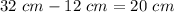
Part D) Find how many square cm greater the rectangle's area is than the square's area if x=4
Find the value of rectangle's area
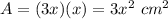 ------>
------>
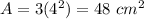
Find the value of square's area
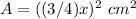 ------>
------>
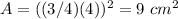
Find the difference
