Question

The solids are similar. Find the surface area S of the red solid. Round your answer to the nearest tenth.

Answer 1

86.6 yd²

Explanation:

When figures are similar, all of the corresponding linear dimensions have the same ratio. The area of each figure is the product of two linear dimensions, so corresponding areas will have a ratio that is the square of the ratio of the linear dimensions.

__

area ratio

In this problem statement, we are given the heights of two similar cuboids. The ratio of the area of the smaller one to the area of the larger one is the square of the ratio of the smaller height to the larger height:

`\frac{\text{smaller area}}{\text{larger area}}=\left(\frac{\text{smaller height}}{\text{larger height}}\right)^2=\left(\frac{6\text{ yd}}{8\text{ yd}}\right)^2=\left((3)/(4)\right)^2=(9)/(16)`

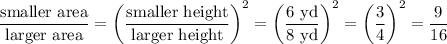
smaller area

The area of the smaller cuboid can be found by multiplying this fraction by the area of the larger cuboid:

`\text{smaller area}=\text{(larger area)}*(9)/(16)=(154\text{ yd}^2)*(9)/(16)\\\\=86(5)/(8)\text{ yd}^2\approx\boxed{86.6\text{ yd}^2}`

The surface area of the red solid is about 86.6 square yards.