Question

The area of a rectangle is 480in^2 . the length is 4 more than the width. Find each measurement.

Answer 1

width = 20 in

length = 24 in

Explanation:

A = 480

L = 4 + w

w

A = L x w

A = (4 + w)w

A = 4w +
`w^(2)`

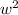
480 = 4w +
`w^(2)`

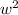
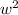`w^(2)` + 4w - 480 = 0

(w + 24)(w - 20) = 0

w = -24 or w = 20

length can't be negative, so w = 20

if w = 20,

L = 4 + w

L = 4 + 20

L = 24

Check:

A = L x w

A = 24 x 20

A = 480