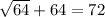Question

The square of a number plus the number is 72. Find the number(s)

Answer 1

The answer would be 8, 8 times 8 is 64 plus 8 is 72

Answer 2

Answer: x = 64[/tex]

Explanation:

In mathematical notation, the problem is to solve the following equation

`√(x) + x = 72`

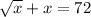
We can assume that the new variable is
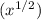`(x^(1/2))`, so the equation is:

`(x^(1/2) )^(2) + (x^(1/2) ) -72 = 0`

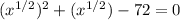
We can solve this like a normal quadratic equation

`x^(1/2) = (-1±√(1-4(1)(-72)))/(2)`

`x^(1/2)  = (-1±17)/(2)`,

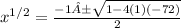
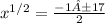The solutions are

`x^(1/2) = -9 \\ x^(1/2) = 8`

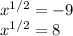
We use the positive one, because a square can not be negative

So,
`x^(1/2) = 8, x = 64`

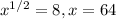
To prove the answer

`√(64) + 64 = 72`