Question

write the standard form of the equation of the circle for which the endpoints of a diameter are (0,0) and (4,-6)

Answer 1

Given:

The endpoints of a diameter are (0,0) and (4,-6).

To find:

The equation of the circle.

Solution:

The endpoints of a diameter are (0,0) and (4,-6). So, the length of the diameter is

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

`d=√((-6-0)^2+(4-0)^2)`

`d=√(36+16)`

`d=√(52)`

`d=2√(13)`

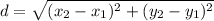
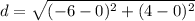
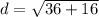
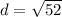
Now, radius is half of the diameter.

`r=(2√(13))/(2)`

`r=√(13)`

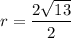
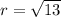
Center of the circle is the midpoint of the endpoints of a diameter.

`Center=\left((x_1+x_2)/(2),(y_1+y_2)/(2)\right)`

`Center=\left((0+4)/(2),(0+(-6))/(2)\right)`

`Center=\left((4)/(2),(-6)/(2)\right)`

`Center=\left(2,-3\right)`

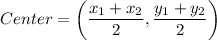
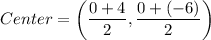
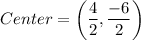
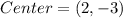
Standard form of a circle is

`(x-h)^2+(y-k)^2=r^2`

where, (h,k) is center and r is radius.

The center of the circle is (2,-3) and radius is
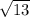`√(13)`. So,

`(x-2)^2+(y-(-3))^2=(√(13))^2`

`(x-2)^2+(y+3)^2=13`

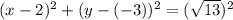
Therefore, the standard form of the circle is
`(x-2)^2+(y+3)^2=13`.