Question

Each cone of the hourglass has a height of 18 millimeters. The total height of the sand within the top portion of the hourglass is 54 millimeters. The radius of both cylinder and cone is 8 millimeters. Sand drips from the top of the hourglass to the bottom at a rate of 10π cubic millimeters per second. How many seconds will it take until all of the sand has dripped to the bottom of the hourglass?

68.3
38.4
268.8
230.4

Answer 1

268.8 seconds

Explanation:

The top portion and the bottom is congruent but rotated 180° of the hourglass is a figure equivalent to a cylinder on top and a cone on bottom.

The total volume contained in the top portion = Volume of a cylinder + the Volume of a cone.

Since we are given that Each cone of the hourglass has a height of 18 millimeters. The total height of the sand within the top portion of the hourglass is 54 millimeters.

So, Height of the cylinder is 54 mm - 18 mm = 36 mm

The formula for the volume of a cylinder is V =
`\pi r^2 h`

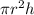
Since we are given that The radius of both cylinder and cone is 8 millimeters.

So, radius = 8 mm

Height = 36 mm

Substitute the values in the formula

So,
`V=\pi 8^2 * 36`

`V=2304\pi`

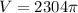
The formula for the volume of a cone is V =
`(1)/(3) \pi r^2 h`

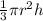
Radius = 8 mm

Height = 18 mm

Substitute the values in the formula

`V=(1)/(3) \pi 8^2 * 18`

`V=384 \pi`

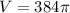
Now, The total volume of the top portion=Volume of the cylindrical part + volume of the cone:

Total volume =
`2304 \pi + 384 \pi=2688 \pi`

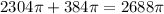
Now to find the number of seconds it take until all of the sand has dripped to the bottom of the hourglass you have to divide the total volume of sand by the rate:

`\text{time in seconds} =\frac{\text{ total volume of sand }}{\text{ rate of dripping}}`

Since we are given that Sand drips from the top of the hourglass to the bottom at a rate of 10π cubic millimeters per second.

So,
`\text{time in seconds} =(2688 \pi )/(10 \pi)`

`\text{time in seconds} =268.8`

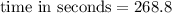
Hence it will take 268.8 seconds until all of the sand has dripped to the bottom of the hourglass

Thus Option C is correct.

Answer 2

Let
Vco------------------- >Volume cone
Vcy------------------ >Volume cylinder
r= 8mm
hco----------- > height of cone=18 mm
hcy------------ > height of cylinder =54-18=36 mm
then
Vco=π*r² *hco/3--------- > π*8² *18/3=π*384 mm³

Vcy=π*r² *hcy--------- > π*8² *36=π*2304 mm³

the total cubic millimeters of sand=Vco+Vcy=π*384+π*2304=π*2688

if 10π cubic millimeters --------------------- > 1 seg
π*2688--------------------------------- X
x=π*2688/10π=268.8 seg

the answer is 268.8 seg