Question

1. ERROR ANALYSIS

Your friend is trying to find the maximum value of P = -x + 6y subject to the
following four constraints.
y ≤−2x +4
y≤x+1
x ≥ 0
y20
a. Explain what error your friend made in the graph below? (1 point)
b. Edit the graph below or paste a screenshot of your corrected graph from
Desmos. (1 point)
List the vertices of the feasible region. (1 point)
d. Use all vertices as you calculate and prove how to maximize the objective
function P? (2 points) to

Answer 1

a. See below.

b. See attachment.

c. (1, 2) (2, 0) (0, 0) (0, 1)

d. The maximum value of P is 11.

Explanation:

`\textsf{Maximize}: \quad P=-x+6y`

`\textsf{Subject to}:\begin{cases}\begin{aligned} \quad y &\leq -2x+4\\y&\leq x+1\\x&\geq 0\\y & \geq 0\end{aligned}\end{cases}`

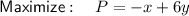
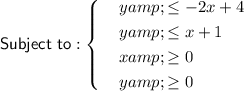
Graph the lines:

`\textsf{Draw the line } \;\;y=-2x+4 \;\;\textsf{and shade under the line}.`

`\textsf{Draw the line } \;\;y=x+1 \;\;\textsf{and shade under the line}.`

`\textsf{Draw the line } \;\;x= 0 \;\;\textsf{and shade above the line}.`

`\textsf{Draw the line } \;\;y=0\;\;\textsf{and shade above (to the right of) the line}.`

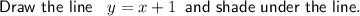
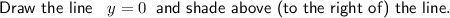
Therefore, the feasible region is bounded by the vertices:

• A = (1, 2)
• B = (2, 0)
• C = (0, 0)
• D = (0, 1)

Determine the value of P at the vertices by substituting the x and y values of the points into the equation for P:

`\textsf{Value of $P$ at $A(1, 2)$}: \quad -(1)+6(2)=11`

`\textsf{Value of $P$ at $B(2, 0)$}: \quad -(2)+6(0)=-2`

`\textsf{Value of $P$ at $C(0, 0)$}: \quad -(0)+6(0)=0`

`\textsf{Value of $P$ at $D(0, 1)$}: \quad -(0)+6(1)=6`

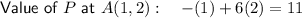
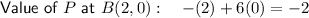
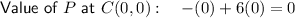
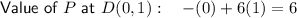
Hence, the maximum value of P is 11 at vertex (1, 2).