Question

Which theorem or postulate proves that △ABC and △DEF are similar?

Select from the drop-down menu to correctly complete the statement.
The two triangles are similar by the ________.

A. AA Similarity Postulate

B. SSS Similarity Theorem

C. SAS Similarity Theorem

Answer 1

Answer: SAS Similarity property

Explanation:

I took the test

Answer 2

△ABC and △DEF are similar by SAS Similarity Theorem.

Option (C) is correct .

Explanation:

Definition of SAS Similarity property

Two triangles are said to be similar by SAS Similarity property If two sides are proportional and one corresponding angle congruent .

In △ABC and △DEF

`(ED)/(AB)= (7)/(21)`

`(ED)/(AB)= (1)/(3)`

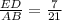
and

`(EF)/(BC)= (11)/(33)`

`(EF)/(BC)= (1)/(3)`

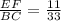
Thus

`(ED)/(AB)=(EF)/(BC)= (1)/(3)`

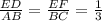
∠ABC = ∠DEF (As given in the figure )

Thus △ABC and △DEF are similar by SAS Similarity property .