Question

So far you have mostly worked with equations. There are special types of equations, called functions, that have exactly one output for every possible input into the equation. An example of this in the real world is the amount of money you are charged at a store: the input is the item you are purchasing, and the output is the money you are charged. Individual items have one price, so this is an example of a function. Can you think of any other examples of functions? Why might this type of equation be useful?

Answer 1

Can you think of any other examples of functions?

Yes! Like putting a check in the bank, that is the input- and then the money you take is the output. You can even use food to compare input and output! Ingredients are the input, and the final dish/dessert is the output. If you wanted something more mathematical, you can use a graph to find the input and output. If you know a few points, you can create a whole line of x and y points, where x= input and y=output. You can also consider getting gas for your car, the money is the input, and the gas (in return) is the output. <== these are just a few examples.

Why might this type of equation be useful?

When you are trying to find the points for a line or looking for the unit price for something, functions can be very useful! You can find what y would be when x equals 1, 2, 3, 4, etc. I know I use this all the time! For example, trying to find the best price for something in the grocery store. There are a lot of options, and if you find the unit price with functions, it makes it easier to get the best deal.

I hope this helps!
~kaikers

Answer 2

There is no certain answer because answer is in words. In mathematical terms

consider f(x) =x + 2, f(x)= x² + 3x +2,

You have to write polynomials having single variable having any degree will be a function.

Explanation:

Real life example :

There are thousands of examples and i am writing few of them.

1. From a set of parents
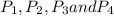`P_(1), P_(2),P_(3) and P_(4)` each having a single child either son or daughter is a function
`S_(1),D_(1),[S_(2) D_(2)], D_(4)`. which is represented as a function , each having a unique outcome
`[P_(1)⇒ S_(1)], [P_(2)⇒ D_(1)],[P_(3)⇒ {S_(2) D_(2)], [P_(4)⇒ D_(4)]`

2. There are different kind of employees in an office or in a system ,or in a country working in government or private sector ranging in Different Grades. Each employee get salary according to rank they possess or the qualification they have.

3. Consider Food you eat and specific nutrients they possess. So, [ Type of Food⇒Nutrients contained in them] are functions.

This type of equation is useful because for each of these examples we can make different equations .Let me make one for you.

Suppose you eat Egg. Represent it by y.it has 4 nutrients (a)Protein (b) Riboflavin (c) Selenium (d) Vitamin.

So if i will write it in terms of equation we can write

y =x²+x+2 [ Considering x=1,we get number of nutrients possessed by egg]

So,by this way we can say these equations are useful.