Question

Kepler’s third law, P2 = kA3, shows the relationship between a planet’s orbital period (P) and the length of its semi-major axis (A). Which statement is true about Kepler’s law?

A.The orbital period is measured in units of time, and the semi-major axis is measured in units of mass.

B.The value k is constant for each of the eight planets in our solar system.

C.For a body orbiting the Sun, increasing the orbital period increases the length of the semi-major axis.

D.To calculate the value of k for a planet in our solar system, find A3 ÷ P2 for the planet.

Answer 1

The answer is B

Step-by-step explanation:

Answer 2

B.The value k is constant for each of the eight planets in our solar system.

Step-by-step explanation:

Kepler's third law states that the square of orbital period of the planet is proportional to the cube of semi-major axis.

P² = k A³

k is constant for all the planets in the solar system.

`k = (4\pi ^2)/(GM)`

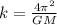
Where, G is the gravitational constant and M is the mass of the Sun.

The orbital period is measured in units of time, and the semi-major axis is measured in units of distance.

With increase in length of the semi-major axis, the orbital period increases.

The value of k can be found by: P²÷A³.