Question

Fiona is purchasing a condominium and is financing $305,000 with a 30-year 5/1 ARM at 4.65% with a 1/12 cap structure. What will her payments be at the beginning of year 6?

(please show your work)

Answer 1

$1736.26

Explanation:

Answer 2

Total amount that has to be paid after 30 years = $305,000 with a 30-year 5/1 ARM at 4.65% with a 1/12 cap structure.

As, amount will depreciate after each year.

Amount left after 6 years which is to be paid=

`Amount = Principal * [1-(rate)/(100)]^(time)\\\\A= 305,000* [1-(4.65)/(100)]^(6)\\\\ A=305,000* [(95.35)/(100)]^(6)\\\\ A=305,000* [0.9535]^(6)\\\\ A=229204.966`

Amount Paid after 6 years = $ 305,000.00 - $ 229204.966

=$ 75795.034

Amount left, after 5 years which is to be paid=

`Amount = Principal * [1-(rate)/(100)]^(time)\\\\A= 305,000* [1-(4.65)/(100)]^(5)\\\\ A=305,000* [(95.35)/(100)]^(5)\\\\ A=305,000* [0.9535]^(5)\\\\ A=240382.76`

Amount paid after 5 years= $ 305,000.00 - $ 240382.76

=$ 64617.24

Total amount that has to be paid between 5 to 6 years= $ 75795.034 - $ 64617.24=$ 11177.794

Monthly payment=

`(11177.794)/(12)\\\\ =931.48`

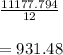
So, monthly payment at the beginning of year 6= $ 931.48