Question

Simplify the radical:

`√(5x^4)`/
`√(10x)`

Answer 1

Split up the top and bottom into factors and cancel out any common factors.

While we do these problems, it is important to remember this rule:


`√(ab) = √(a) √(b)`

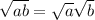
First, we will split up the top.


`√(5x^4) = √(5) √(x^4)`

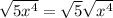
We can't do anything with the square root of 5 because it is in it's simplest form. But, we can still split up the square root of
`x^2`


`√(5) √(x^4) = √(5) √(x^2) √(x^2)`

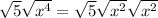
Now we can simplify.


`√(5) √(x^2) √(x^2) = √(5) x * x`


`√(5) x * x = √(5)x^2`

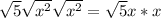
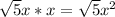
The top is done, now for the bottom one.


`√(10x) = √(10) √(x)`

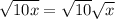
We can't simplify either the square root of 10 or the square root of x.
So, the top is done, too.

Find any common factors and cancel them out.


`(√(5)x^2)/(√(10) √(x))`

Well, I can't find any common factors to cancel out, but, we can still simplify it further.

There is another law regarding radical expressions:


`\sqrt{(a)/(b)} = (√(a))/(√(b))`

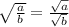
Using this, simplify the expression further.


`(√(5)x^2)/(√(10) √(x)) = \sqrt{(5)/(10)} (x^2)/(√(x))`


`\sqrt{(5)/(10)} (x^2)/(√(x)) = \sqrt{(1)/(2)} (x^2)/(√(x))`

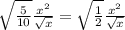
So, now it is in it's simplest form.