Answer:
Solving the similar triangles, we get x=10.6, y=66
Explanation:
The triangles are similar.
We need to find the values of x and y
If the triangles are similar, the ratio of corresponding sides is equal.
So, we can write:
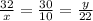
Now, we can solve to find value of x and y
First solving to find value of x:
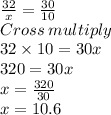
So, we get x = 10.6
Now, finding value of y:
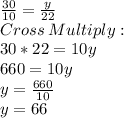
So, we get y = 66
Solving the similar triangles, we get x=10.6, y=66