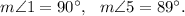Question

Which of the following statements help prove that calypso rd and capoeira rd are parallel?

Answer 1

did anyone reply? plzzzz let me know

Answer 2

Answer: The answers are given below.

Step-by-step explanation: We are given two straight lines calypso rd and capoeira rd. Both are cut with a transversal Lambda Ave. We are select all the correct conditions from the given options that will help to prove that lines calypso rd and capoeira rd are parallel to each other.

Condition (1) is

`m\angle 2=81^\circ,~~m\angle 3=89^\circ.`

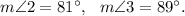
Since ∠2 and ∠3 are interior angles on the same side of the transversal and their sum is 81° + 89° = 170° ≠ 180°, so this condition will not help.

Condition (2) is

`m\angle 1=90^\circ,~~m\angle 5=90^\circ.`

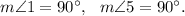
Since ∠1 and ∠3 are vertically opposite angles and ∠3 and ∠5 are corresponding angles, so we have m∠1 = m∠3 = m∠5, so this condition will help.

Condition (3) is

`m\angle 4=85^\circ,~~m\angle 5=85^\circ.`

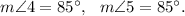
Since the measurement of ∠4 and ∠5 do not have anything related to prove the parallelism of the given lines, so this condition will not help.

Condition (4) is

`m\angle 2+m\angle 6=180^\circ.`

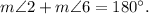
Since ∠2 and ∠6 are corresponding angles, so their measurement shoul be equal in order to prove the lines parallel. vAs our given condition does not imply this, so this condition will also not help.

Condition (5) is

`m\angle 2+m\angle 3=180^\circ.`

Since ∠2 and ∠3 are interior angles on the same side of the transversal, and their sum is given to be 180°, so this condition implies that the two lines are parallel. Hence, this condition will help.

Condition (6) is

`m\angle 3+m\angle 4+m\angle 5+m\angle 6=360^\circ.`

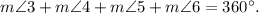
Since this is the general condition that the measurement of the whole angle is 360°, so this condition will not help.

Condition (6) is

`m\angle 1=m\angle 3=m\angle 5.`

Since ∠1 and ∠3 are corresponding angles and ∠3 and ∠5 are alternate interior angles, so their equality will definitely help in proving the lines to be parallel.

Thus, the correct conditions are

`m\angle 1=90^\circ,~~m\angle 5=89^\circ.`

`m\angle 2+m\angle 3=180^\circ.`

`m\angle 2+m\angle 3=180^\circ.`

`m\angle 1=m\angle 3=m\angle 5.`