Question

Please give me the correct answer ​

Answer 1

PQ = 5 units

QR = 8 units

Explanation:

Given

P(-3, 3)

Q(2, 3)

R(2, -5)

To determine

The length of the segment PQ

The length of the segment QR

Determining the length of the segment PQ

From the figure, it is clear that P(-3, 3) and Q(2, 3) lies on a horizontal line. So, all we need is to count the horizontal units between them to determine the length of the segments P and Q.

so

P(-3, 3), Q(2, 3)

PQ = 2 - (-3)

PQ = 2+3

PQ = 5 units

Therefore, the length of the segment PQ = 5 units

Determining the length of the segment QR

Q(2, 3), R(2, -5)

(x₁, y₁) = (2, 3)

(x₂, y₂) = (2, -5)

The length between the segment QR is:

`l=√(\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2)`

`=√(\left(2-2\right)^2+\left(-5-3\right)^2)`

`=√(0+8^2)`

`=√(8^2)`

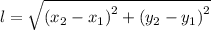
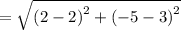
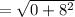
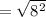
Apply radical rule:
`\sqrt[n]{a^n}=a,\:\quad \mathrm{\:assuming\:}a\ge 0`

`=8`

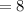
Therefore, the length between the segment QR is: 8 units

Summary:

PQ = 5 units

QR = 8 units