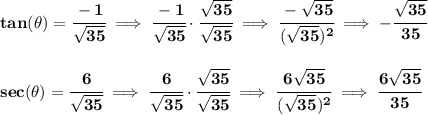Question

Find the remaining trigonometric ratios of θ if csc(θ) = -6 and cos(θ) is positive

Answer 1

now, the cosecant of θ is -6, or namely -6/1.

however, the cosecant is really the hypotenuse/opposite, but the hypotenuse is never negative, since is just a distance unit from the center of the circle, so in the fraction -6/1, the negative must be the 1, or 6/-1 then.

we know the cosine is positive, and we know the opposite side is -1, or negative, the only happens in the IV quadrant, so θ is in the IV quadrant, now


`\bf csc(\theta)=-6\implies csc(\theta)=\cfrac{\stackrel{hypotenuse}{6}}{\stackrel{opposite}{-1}}\impliedby \textit{let's find the \underline{adjacent side}} \\\\\\ \textit{using the pythagorean theorem}\\\\ c^2=a^2+b^2\implies \pm√(c^2-b^2)=a \qquad \begin{cases} c=hypotenuse\\ a=adjacent\\ b=opposite\\ \end{cases} \\\\\\ \pm√(6^2-(-1)^2)=a\implies \pm√(35)=a\implies \stackrel{IV~quadrant}{+√(35)=a}`

recall that


`\bf sin(\theta)=\cfrac{opposite}{hypotenuse} \qquad\qquad cos(\theta)=\cfrac{adjacent}{hypotenuse} \\\\\\ % tangent tan(\theta)=\cfrac{opposite}{adjacent} \qquad \qquad % cotangent cot(\theta)=\cfrac{adjacent}{opposite} \\\\\\ % cosecant csc(\theta)=\cfrac{hypotenuse}{opposite} \qquad \qquad % secant sec(\theta)=\cfrac{hypotenuse}{adjacent}`

therefore, let's just plug that on the remaining ones,


`\bf sin(\theta)=\cfrac{-1}{6} \qquad\qquad cos(\theta)=\cfrac{√(35)}{6} \\\\\\ % tangent tan(\theta)=\cfrac{-1}{√(35)} \qquad \qquad % cotangent cot(\theta)=\cfrac{√(35)}{1} \\\\\\ sec(\theta)=\cfrac{6}{√(35)}`

now, let's rationalize the denominator on tangent and secant,


`\bf tan(\theta)=\cfrac{-1}{√(35)}\implies \cfrac{-1}{√(35)}\cdot \cfrac{√(35)}{√(35)}\implies \cfrac{-√(35)}{(√(35))^2}\implies -\cfrac{√(35)}{35} \\\\\\ sec(\theta)=\cfrac{6}{√(35)}\implies \cfrac{6}{√(35)}\cdot \cfrac{√(35)}{√(35)}\implies \cfrac{6√(35)}{(√(35))^2}\implies \cfrac{6√(35)}{35}`