Question

It takes a printer 10 hours to print the class schedules for all of the students in a college. A faster printer can do the job in 6 hours. How long will it take to do the job if both printers are used?

Answer 1

if for the slower printer it takes 10 hours for the whole thing, how much has it done in 1 hour? well, since it takes 10 hours total, in 1 hour it has only done 1/10 th of the whole work.

the faster printer however, can do it in 6 total, how much has it done in 1 hour? well, 1/6 of the whole work.

now, let's say, they both work together, and it takes "t" hours to finish the whole thing with both rolling.

let's add both rates to see how much that is,


`\bf \stackrel{slower~printer}{\cfrac{1}{10}}~~+~~\stackrel{faster~printer}{\cfrac{1}{6}}~~=~~\stackrel{1hr~work}{\cfrac{1}{t}}\\\\ -------------------------------\\\\ \textit{LCD is 30}\implies \cfrac{3+5}{30}=\cfrac{1}{t}\implies \cfrac{8}{30}=\cfrac{1}{t}\implies t=\cfrac{30\cdot 1}{80}`

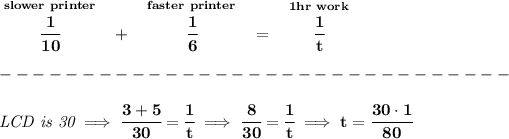
which is 3 hours and 45 minutes.