Answer:
π
Explanation:
General form of the cosine function is:
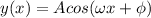
Where:
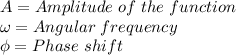
The frequency of the function is given by the following equation:
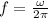
The period is the reciprocal of the frequency, so:

From the equation provided, you can see that the angular frequency is 2. Therefore, the periodof the function is:
