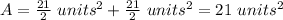Question

What is the area of parallelogram RSTU?

Answer 1

I may be wrong but it could be C.

Answer 2

The answer is the option
`21\ units^(2)`

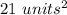
Explanation:

we know that

In this problem the area of parallelogram RSTU is equivalent to the sum of the area of the right triangle RUS and the area of the right triangle UST

Remember that

The area of a triangle is equal to

`A=(1)/(2)bh`

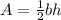
Find the area of triangle RUS

we have

`b=US=7\ units` -----> observing the figure

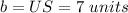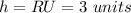`h=RU=3\ units` -----> observing the figure

substitute

`A1=(1)/(2)(7)(3)=(21)/(2)\ units^(2)`

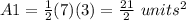
Find the area of triangle UST

we have

`b=US=7\ units` -----> observing the figure

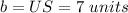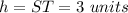`h=ST=3\ units` -----> observing the figure

substitute

`A2=(1)/(2)(7)(3)=(21)/(2)\ units^(2)`

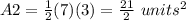
The area of parallelogram is the sum of the area of two triangles

so

`A=A1+A2`

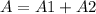
substitute

`A=(21)/(2)\ units^(2)+(21)/(2)\ units^(2)=21\ units^(2)`